![[Algorithm] 알고리즘의 복잡도와 Big-O 란?](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FdtgKJW%2FbtqURuspKkk%2F1hcqY9Khq8n2O4wBpD2rG1%2Fimg.jpg)
알고리즘이란
- 어떤 목적을 달성하거나 결과물을 만들어내기 위해 거쳐야 하는 일련의 과정들의 집합을 의미한다.
- 가는 루트는 다양하며 여러가지 상황에 따른 알고리즘은 모두 다르다. 따라서 시간복잡도가 가장 낮은 알고리즘을 선택하여 사용한다.
복잡도(Complexity)는 알고리즘의 성능을 나타내는 척도이다. 복잡도는 시간 복잡도와 공간 복잡도로 나눌 수 있다.
시간 복잡도
특정한 크기의 입력에 대하여 알고리즘을 수행할 때 연산이 몇번 이루어지는 지를 표기
공간 복잡도
특정한 크기의 입력에 대하여 알고리즘이 얼마나 많은 메모리를 차지하는지를 의미
동일한 기능을 수행하는 알고리즘이 있다면 일반적으로 복잡도가 낮을수록 좋은 알고리즘이다.
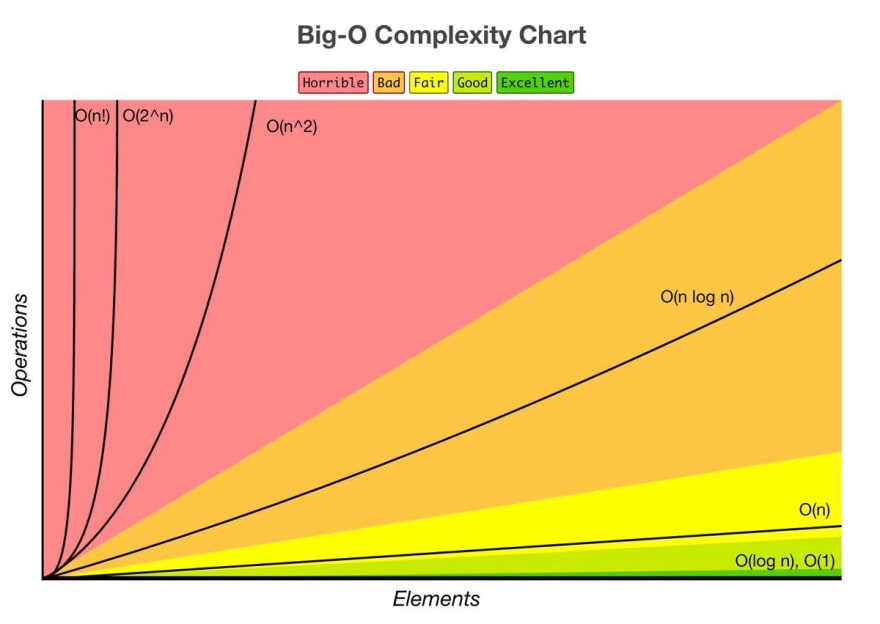
빅오 표기법(Big O Notation)
복잡도를 표현할때에는 빅오 표기법을 사용한다. 빅오 표기법은 가장빠르게 증가하는 항만을 고려하는 표기법이다.
다시 말해 함수의 상한만을 나타낸다.
시간복잡도에서 중요하게 보는것은 가장큰 영향을 미치는 n의 단위이다.
시간복잡도의 문제해결 단계를 나열 하면 아래와같다.
| 빅오 표기법 | 명칭 | N이 1,000일 때의 연산 횟수 |
| O(1) | 상수시간 : 문제를 해결하는데 오직 한 단계만 처리함. | N/A |
| O(logN) | 로그 시간 : 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듬. | N/A |
| O(N) | 선형 시간 : 문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가짐. | 1,000 |
| O(NlogN) | 로그 선형 시간 : 문제를 해결하기 위한 단계의 수가 N*(log2N) 번만큼의 수행시간을 가진다. | 10,000 |
| O(N^2) | 이차 시간 : 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱. | 1,000,000 |
| O(N^3) | 삼차 시간 : 문제를 해결하기 위한 단계의 수는 입력값 n의 세제곱. | 1,000,000,000 |
| O(2^N) | 지수 시간 : 문제를 해결하기 위한 단계의 수는 주어진 상수값 C 의 n 제곱. | 10715086071... |
정렬 알고리즘 비교
| Sorting Algorithms | 공간 복잡도 | 시간 복잡도 | ||
| 최악 | 최선 | 평균 | 최악 | |
| Bubble Sort | O(1) | O(n) | O(n2) | O(n2) |
| Heap Sort | O(1) | O(n log n) | O(n log n) | O(n log n) |
| Insertion Sort | O(1) | O(n) | O(n2) | O(n2) |
| Merge Sort | O(n) | O(n log n) | O(n log n) | O(n log n) |
| Quick Sort | O(log n) | O(n log n) | O(n log n) | O(n2) |
| Selection Sort | O(1) | O(n2) | O(n2) | O(n2) |
| Shell Sort | O(1) | O(n) | O(n log n2) | O(n log n2) |
| Smooth Sort | O(1) | O(n) | O(n log n) | O(n log n) |
자료구조 비교
| Data Structures | Average Case | Worst Case | ||||
| Search | Insert | Search | Insert | Delete | ||
| Array | O(n) | N/A | N/A | O(n) | N/A | N/A |
| Sorted Array | O(log n) | O(n) | O(n) | O(log n) | O(n) | O(n) |
| Linked List | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Doubly Linked List | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Stack | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Hash table | O(1) | O(1) | O(1) | O(n) | O(n) | O(n) |
| Binary Search Tree | O(log n) | O(log n) | O(log n) | O(n) | O(n) | O(n) |
| B-Tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| Red-Black tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| AVL Tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
'Algorithm > Theory' 카테고리의 다른 글
| [Algorithm] DP (Dynamic Programming) : 동적 계획법 (0) | 2021.03.11 |
|---|---|
| [Algorithm] 탐색 알고리즘 DFS/BFS (0) | 2021.01.29 |
| [Algorithm] 구현(Implementation) (0) | 2021.01.28 |
| [Algorithm] 그리디(Greedy) : 탐욕법이란? (0) | 2021.01.27 |